3-3. 2段研磨研磨と3段研磨プロセス最適解の比較
3-3-1. (A)式を用いた場合
2段研磨の最適研磨時間と3段研磨の最適研磨時間を比較し、どういう条件の時に2段研磨の最適研磨時間が速くなり、どういう条件の時に3段研磨の最適研磨時間が優位になるかを考察します。すでに、1段研磨解と2段研磨解を比較し、2段研磨解が優位になる条件は連載(2)で考察しました。また3段研磨の2段目の研磨の速度が、最終段の3段研磨よりも遅くなってしまう場合についても、前節の3-2-1.や3-2-2.で考察しました。ここではさらに、単純に3段研磨と、3段研磨の2段研磨工程を省略した2段研磨と比較し、3段研磨が優位になる条件を考えます。
最初に加工変質層の厚みと研磨速度の関係が(A)式で示すことができる場合を想定します。2段研磨の粗研磨と仕上げ研磨の装置や研磨剤は3段研磨の粗研磨と仕上げ研磨の装置や研磨剤と同じものを使うこととします。2段研磨の比例定数a1とa2は3段研磨のパラメタと同じに揃えるためにa1,a3と書き換えます。パラメタのa2は3段研磨の中間研磨の研磨条件にのみ使うこととします。そして洗浄時間は無視して比較し、後から洗浄時間を考慮します。
そうすると、3段研磨が2段研磨より高速になる条件は、
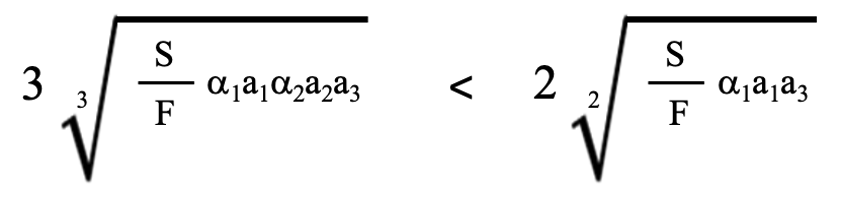
(3-11)
と示すことができます。(3-11)式の左辺は(3-5)式そのもので、右辺は(1-6)式そのものです。(3-11)式を変形すると、
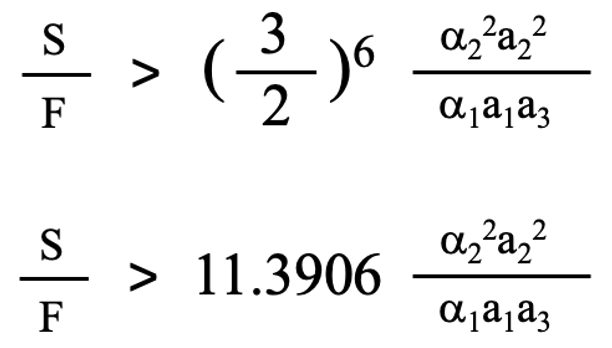
(3-12)
S/Fがある臨界値を超えると、3段研磨が速くなることがわかります。ここでSは1段目の研磨プロセスで削り落とさねばならない最初に設定された厚みです。Fは仕上げの研磨によって最終的に残った加工変質層の厚みです。つまり目標とする薄い最終加工変質層の厚みです。Sの値が大きいほど、あるいはFの値が小さいほど、あるいはS/Fが大きいほど、3段研磨が有利であると推察されます。(3.11)式を図示すると図3-2(a)のようになります。
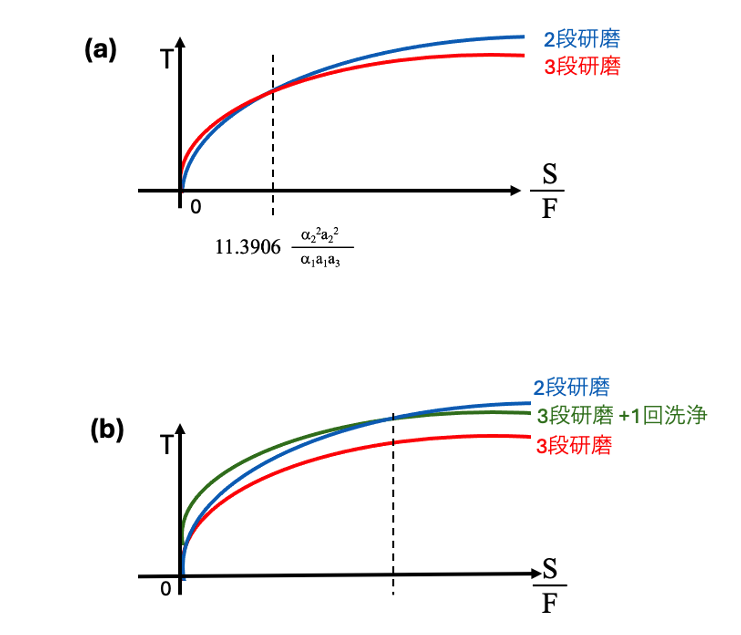
図3-2 は 2段研磨と3段研磨の場合の研磨時間の比較を示した図です。縦軸は全研磨時間、横軸はS/Fの値で示しています。横軸のS/Fの値は、より薄いFの値を目標とすると、より大きな値になります。図3-2(a)は洗浄時間を無視した2段研磨と3段研磨の場合の研磨時間です。S/Fが大きくなると3段研磨の研磨時間が短くなり、3段研磨が有利になります。実際の研磨作業では3段研磨の場合3回洗浄を行い、2段研磨の場合2回洗浄を行います。3段研磨の場合は1回余分に洗浄時間が加わります。図3-2(b)では赤線の3段研磨時間に、1回の洗浄時間を足したものを緑の線で示しています。赤い曲線は1回の洗浄時間分のみ上側に平行移動して緑の曲線にしています。1回分の洗浄時間を足し合わせたものと比較すると、S/Fの値がさらに大きなところで3段研磨が有利になるということが、図3-2(b)ではわかります。
(3-11)式のα1,α2,a1,a2,a3などに実際の数値を代入すると、S/Fがかなり小さい値の時に図3-2の2つの曲線は交差している場合の可能性も推察されます。この場合は、3段研磨がほぼ最初から優位になります。また、場合によっては、S/Fがかなり大きい値の時に2つの曲線は交差することになります。この場合、いつまで経っても2段研磨が優位な状況が続き、Fがかなり薄くなってきて優位になってくることもあり得ます。
3-3-2. (B)式を用いた場合
次に加工変質層の厚みと研磨速度の関係が(B)式で表すことができる場合を考察します。3段研磨の2段研磨を省略する2段研磨と比較します。3段研磨が2段研磨より高速になる条件は、
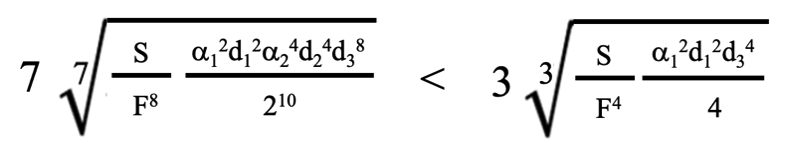
(3-13)
で示されます。(3-13)式の左辺は(3-10)式、右辺は(2-4)式です。これを変形すると
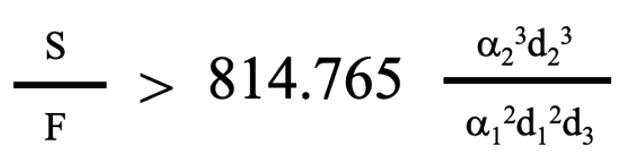
(3-14)
となって、(3-12)式と似た格好の条件が得られます。S/Fがある値以上になると、3段研磨が2段研磨より研磨速度上優位になります。これは、(3-11), (3-12)式と似た結論です。そして3段研磨にさらに洗浄時間を加えると、(3-14)の条件よりも、もっとS/Fの大きなところで、3段研磨が有利になります。図3-2(b)と似たような曲線が得られます。
図3-2で考察された事と同様に、S/Fの値が現実離れした大きな値で2つの曲線が交差点する場合は、2段研磨が有利です。また、S/Fの値が現実離れした小さな値の場所で2つの曲線が交差点する場合は、最初から3段研磨が有利になります。さらに他の、加工変質層の厚みと研磨速度との関係式を使う場合、(3-12)式や(3-14)式を見ると、帰納法的に、ある程度予測がつくと思います。
3-4. PCを用いたシミュレーション
3段研磨の全研磨時間Tはv1とv2の2つのパラメターの関数になっています。実際の研磨の最適化の場合、前もって、各研磨プロセスでの研磨速度と加工変質層の厚みの関係が実験によって調べられていて、既知だとします。つまり、αn Xn(vn)の値は調べられていると仮定します。
エクセルのようなPCソフトによる力技で、Tはv1とv2の関数として求めることはできます。
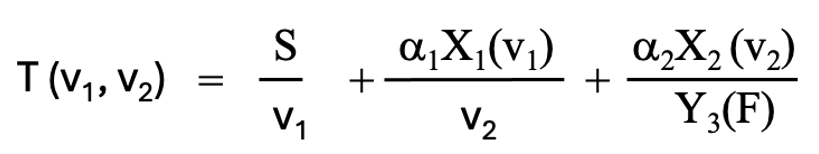
(3-15)
v1,v2の2つのパラメタをランニングパラメタとして振って、Tを最小にするv1、v2を求めることができます。またv3は固定されています。全てPCによる力技で3段研磨の最適条件は簡単に求めることはできます。
3-5. 3段研磨での消耗品費の考察
連載(2)で2段研磨での砥粒や研磨剤などの消耗剤の消耗品費を考察しました。ここでは簡単に3段研磨での消耗品費について考察します。(A)式の場合を想定します。連載(2)で示した消耗モデルをそのまま使います。3段研磨での消耗品費Cを1段目と2段目の研磨速度v1とv2の 関数として示すと(3-16)のように示されます。
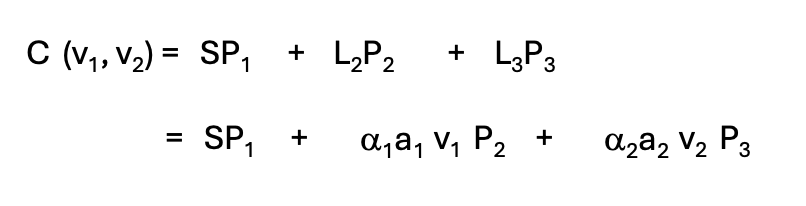
(3-16)
Pnは連載(2)で導入した消耗剤の値段と、研磨されたウエハの厚みとの比例定数です。ウエハの削り落とされた量と、消耗剤の消耗量が比例するというモデルです。2段研磨で考察した結論と同じように、消耗品費は研磨速度v1とv2に依存していることになります。この解説のモデルだとv1とv2を遅くすればするほど消耗品費を抑制することができるという結論が出てきます。各研磨工程の高速化と消耗品費の抑制とは相反する目的だということがわかります。逆に、消耗品費が固定されている場合、消耗品費に対応した研磨速度を設定することはできます。全研磨時間と消耗品費の予測をすることは可能にはなり、調整をすることは一応はできます。また当たり前の話ですが、無駄に消耗剤を消耗させないようにするため、必要以上に研磨は行わないことだということはわかります。
3-6. まとめ
この連載(3)では、3段研磨の最適解について考察しました。簡単に解析的に解ける場合は、加工研磨条件を導きました。(3-4),(3-9)式で示されている各研磨段での研磨速度と研磨時間の組み合わせが3段研磨での最適な研磨条件だと一意的に求めることができました。
また、2段研磨と3段の研磨での全研磨時間を比較すると、F/Sの値が大きくなると3段の研磨時間が有利になることがわかりました。2段研磨が優位なのか3段研磨が優位なのかは、判断することができます。
加工変質層の厚みと研磨速度の関係を前もって実験的に調べると、全研磨時間はPCを使ってエクセルのようなソフトでシミュレーションすることは可能です。また、より精密な実験により、消耗剤の消耗量を測定すれば、より正確な消耗品費のシミュレーションも可能だと思われます。PCを使ったシミュレーションでは、力技によって、消耗品費や研磨の総時間などもシミュレーションが可能なので、研磨会社にとって都合の良い消耗品費や研磨の総時間の組み合わせなどが求められ、最適な研磨のやり方の考察が可能かと思われます。
3段研磨で初段の研磨の際に研磨速度を変えて研磨をすることは4段研磨とみなすことができます。
連載の(4)では、4段研磨について考察します。






