“4H-SiCの積層欠陥(1)”ではショックレー型積層欠陥が1枚導入された場合について、そのショックレー型積層欠陥がいくつかに分類されることを述べまました。“その2”ではショックレー型積層欠陥が複数枚重なっているときの特異な現象などについて述べます。この特異な現象が伴う積層欠陥を過去にはステルス積層欠陥などと呼んだりしていました。G. Feng氏たちは4H-SiCの積層欠陥にショックレー型積層欠陥が1枚導入されているものと、2枚、3枚、4枚導入されているものを、それぞれ1SSF,2SSF, 3SSF, 4SSFなどと名称を付け整理分類しています。これらの多層の積層欠陥はステルスな振る舞いをするものがあり、ちょっと厄介です。以下にこの多層枚ショックレー型積層欠陥のステルスな構造について解説します。
ステルスな積層欠陥
このFengさんの文献で4SSFと定義した積層欠陥は、顕微フォトルミなどの分光的手法を用いた場合、その存在は検出することは可能です。また、透過型電子顕微鏡断面高分解能像観察でも検出することは可能ですが、X線トポグラフ法や透過型電子顕微鏡法で積層欠陥を同定するときに一般的に行われている、いわゆるg・R解析などの基礎的な同定方法では、困ったことに検出することはできません。この文章では話を簡略化して進めます。透過型電子顕微鏡を用いた積層欠陥の同定法や、積層欠陥のコントラストメカニズムなどを詳しく知りたいかたは文末の文献を参照してください。
回折現象を利用して積層欠陥を同定するときの概略を図1で示します。図の赤い点線は積層欠陥を表しています。積層欠陥の両端には緑色の部分転位が存在します。青色の結晶面は回折現象を起こしているg反射の結晶面を示していると想定します。積層欠陥の変位ベクトルをRとすると、Rは積層欠陥の上下での結晶面のずれを示しています。またRは片方の部分転位のバーガース・ベクトルと一致しています。
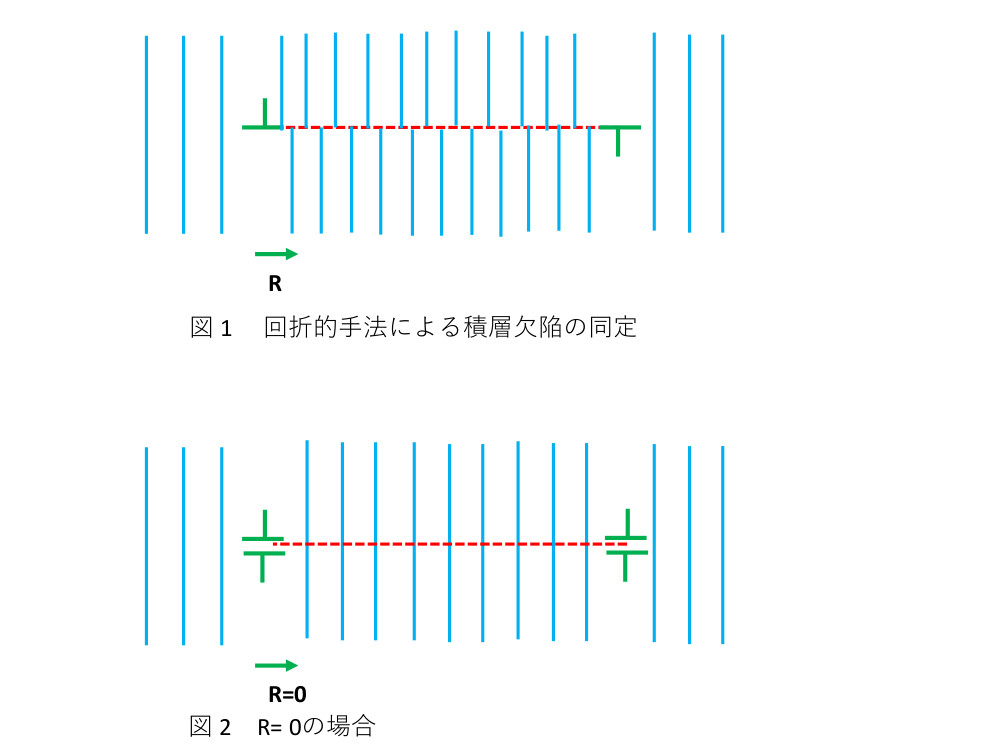
特徴的なことはexp(2πg・R) =1の時、積層欠陥のコントラストは消失します。この時の状態を図2に示します。この性質を利用してgを変えて電子顕微鏡像や、X線トポグラフ像を撮影し、積層欠陥のコントラストが消滅する反射を見つけ出すと積層欠陥の変位ベクトルRを同定することができて、その積層欠陥が何であるかを議論することができます。ちなみに積層欠陥の縁に付随している部分転位のバーガース・ベクトルbとgベクトルの内積g・bが値を持っていると積層欠陥の縁にある部分転位はコントラストがついていますが、そのg反射でg・R= integerであれば積層欠陥のコントラストは消失していることには注意が必要で、g・bとg・Rのコントラスト出現と消失は同じルールではありません。
図3にFengさんの文献のFig 4に描かれている4SSFの積層の状態の模式図を示します。図3(a)は完全結晶で積層欠陥が導入されていない状態です。4本の水平な破線は4枚の積層欠陥が導入される位置を示しています。図3(b)は4枚の積層欠陥が導入された状態を示しています。4枚の積層欠陥の変位ベクトル 、R1, R2, R3, R4が2つずつ逆方向を向いてキャンセルされていてトータルでR=0になっています。この状態を図2に示します。この場合、積層欠陥の上と下では回折をおこしている結晶面のずれが生じないので、いくらgベクトルを変えても積層欠陥のコントラストは出現しません。また同様に、4枚の積層欠陥の縁に付属している4本のショックレー型部分転位が近距離に存在している場合、トータルのバーガース・ベクトルはb=b1+b2+b3+b4=0となってしまい部分転位は4本存在しているのに、いくらgベクトルを変えてもこれらの4本の部分転位は電子顕微鏡像やX線トポグラフ像では観察されないことになります。このような4SSFの場合、顕微フォトルミなどの分光学的手法、または透過型電子顕微鏡断面高分解能像では検出することが可能です。
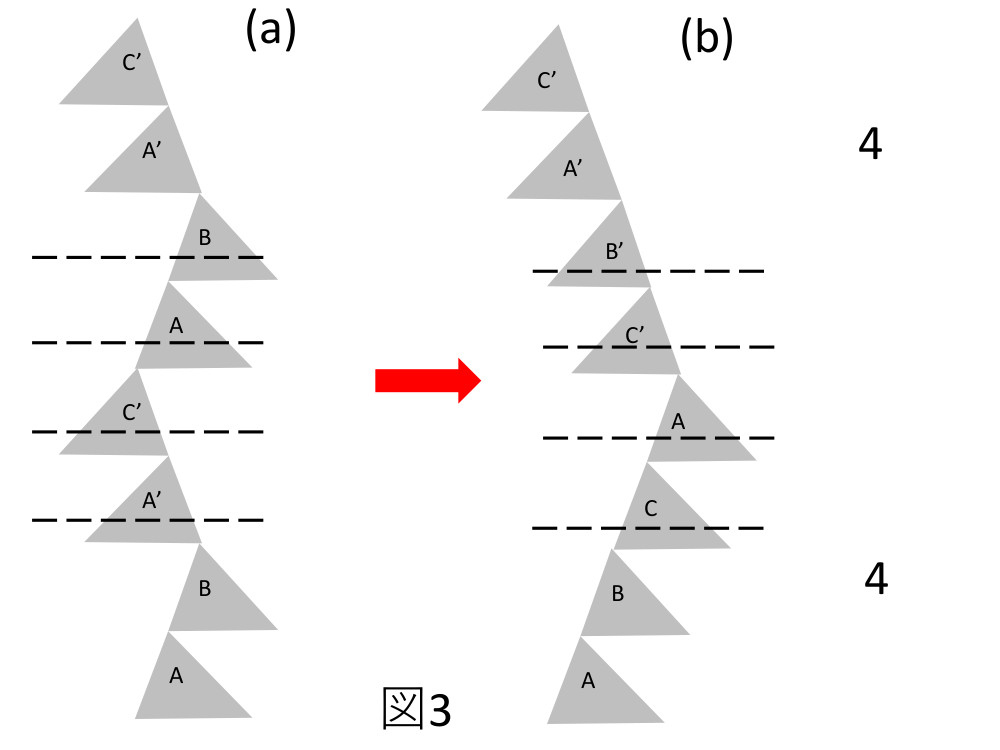
積層欠陥の淵に存在する4本のショックレー型部分転位がばらけて配置していると、それぞれが独立して観察され、1本目の部分転位で1枚のショックレー型積層欠陥が終端すると、残りは3SSF状態になり積層欠陥のコントラストが出現することになります。
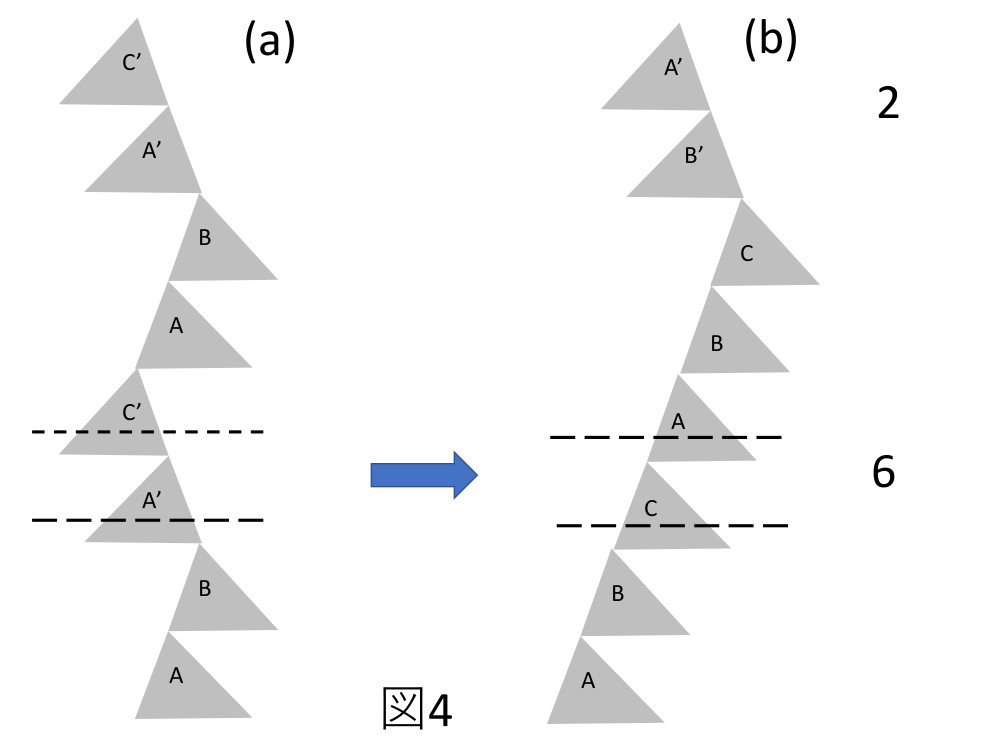
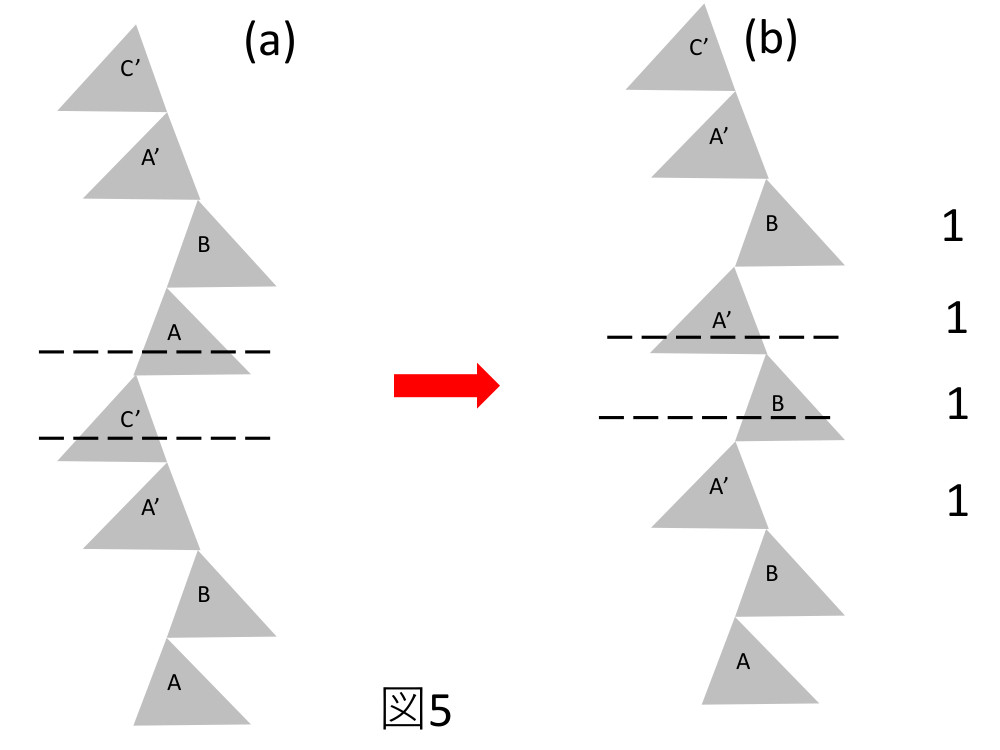
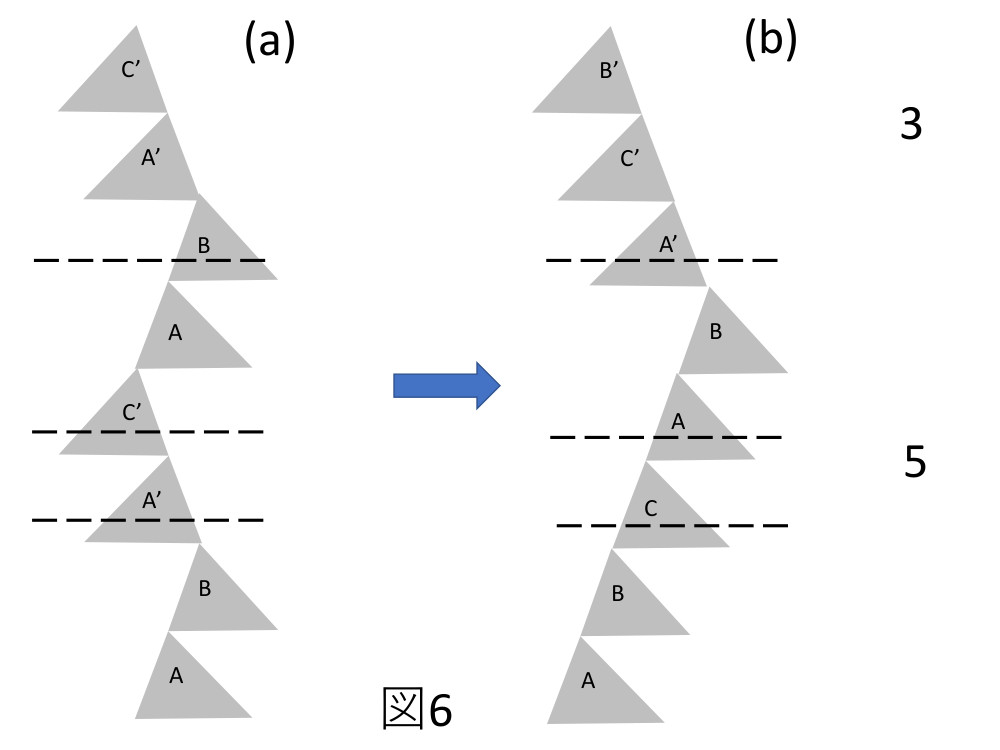
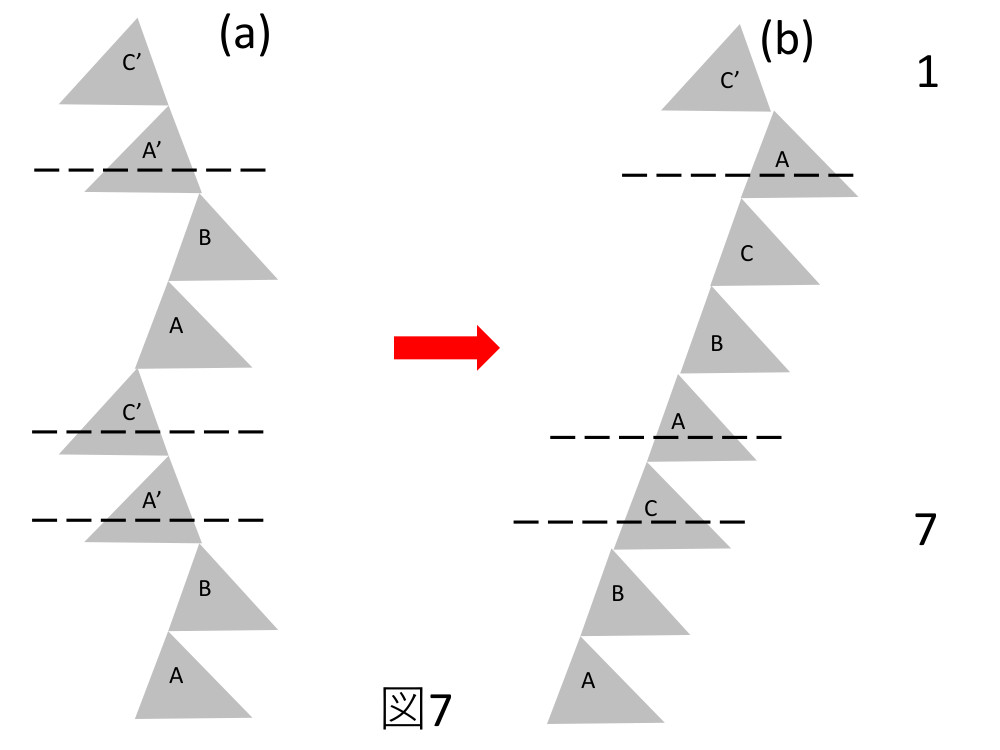
Fengさんの文献の2SSF, 3SSFはR=0ではありませんが、単純に考えると、2SSF, 3SSFでもR=0になる多数枚のショックレー型積層欠陥の構造は可能です。Fengさんの文献では、2SFFの積層欠陥はZhdanovのノーテーションで(6,2)という状態が示されていますが、同じ2SFFでも(1,1,1,1)という状態も可能です。Feng氏の2SSF(6,2)の積層欠陥の構造を図4に示します。図4(a)は完全結晶の場合の積層状態を示しています。破線は積層欠陥が導入される位置です。図4(b)は2枚の積層欠陥が導入された(6,2)の状態を示しています。図5は2枚の積層欠陥が導入された2SSFの状態ですが積層欠陥の導入される位置が図4とは異なっていています。この場合2つの積層欠陥の変位ベクトルは相殺されてR=0の状態になることが可能です。この積層欠陥はg・R解析を行っても、積層欠陥の像コントラストは現れることはありません。この2SFF(1,1,1,1)の場合フォトルミのスペクトルは現れると思いますが、Fengさんの実験で示している2SFFのスペクトルとは異なるはずです。また3SSFの積層欠陥でもFengさんは3SSF(5,3)の報告例を示していますが、3SSF(7,1)となる構造では3つのショックレー型積層欠陥の変位ベクトルが相殺されてしまいR=0が出現し、これらの積層欠陥はX線トポグラフや透過型電子顕微鏡の2波の観察条件で存在を確認することができなくなります。Fengさんの3SSF(5,3)を図6に示します。またステルスな3SSFを図7に示します。積層欠陥が存在するとパワーデバイスにネガティブなインパクトを与えるので厄介な存在と考えられます。検出のためには顕微フォトルミの利用が必要です。
Fengさんの文献および関連文献
- G. Feng et al., Appl. Phys. Lett. 94, 091910 (2009).
- S. Izumi et al., Appl. Phys. Lett. 86, 202108 (2005).
透過型電子顕微鏡の積層欠陥像のコントラストについて記述は下記を参考にして下さい。X線トポグラフ法の場合も、同じコントラストメカニズムで考えることができます。
- Electron microscopy of thin crystals; P. Hirsch, A. Howie, R. Nicolson, D. W. Pashley. M. J. Whelan, Butterworths, pp222-246, (1965).
- Diffraction and imaging techniques in materials science Vol. 1 second revised edition; S. Amerinckx eds, M. J. Whelan, North-Holland pp70-88, (1978).
- Transmission electron microscopy; C. B. Williams & C. B. Carter, Plenum Press, 1st Edition, pp381-399 (1996).






