5-4. 多段加工工程の加工時間の比較
連載(3)で、2段研磨と3段研磨の最適解の比較を行い、3段研磨の最適な組み合わせ解が2段研磨の最適解よりも優位になる条件を示しました。結論としてはS/Fの値が大きくなると、3段研磨の適切解が2段研磨の適切解よりも速いことがわかりました。4段研磨と5段研磨の最適解の比較を行い、5段研磨の最適解が4段研磨の最適解より優位になる条件を考察します。比較の条件を揃えるために、5段研磨の2段目を省略した4段研磨の適切解と5段研磨と適切な組み合わせ解を比較します。また、研磨速度と加工変質層の関係は、(A)式を想定します。話を簡単にするために洗浄時間は考慮しないこととして比較します。
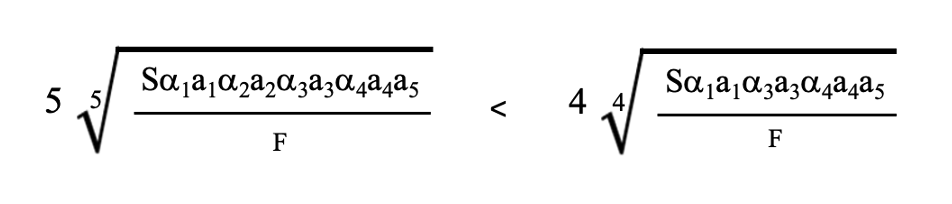
と設定することができて、これを変形すると
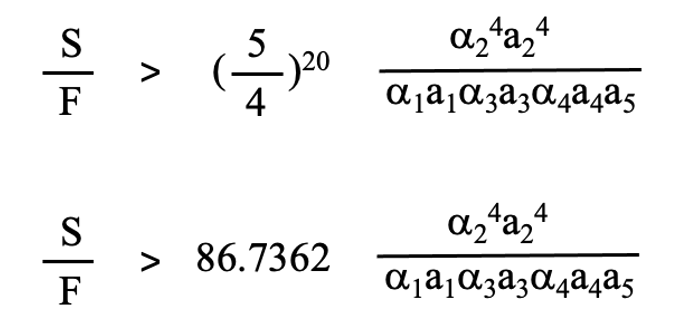
(5-7)
とする条件が出てきます。つまりS/Fの値が、ある臨界値より大きいところで5段研磨が4段研磨よりも速くなります。この条件と、4段研磨の適切な組み合わせ解が3段研磨の適切な組み合わせ解よりも速くなる条件、下記の(5-8)式と、3段研磨の適切な組み合わせ解が2段研磨の適切な組み合わせ解よりも速くなる条件、つまり下記の(3-12)式とを比較してみます。
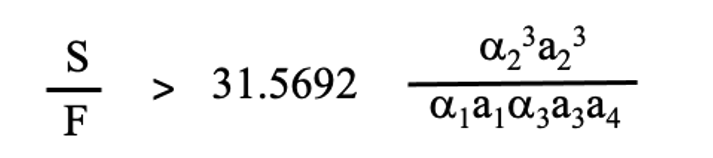
(5-8)
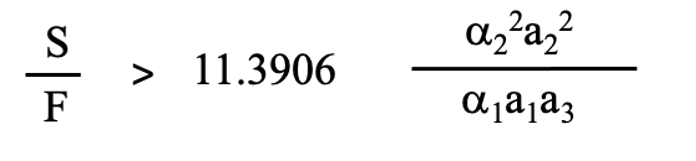
(3-12)
これらの不等式は、αnanについての具体的な数値が入っていないと実際には比較はできないのですが、単純に比較すると、S/Fの値が大きくなって、ある臨界値を超えると3段研磨の適切な組み合わせ解が2段研磨の適切な組み合わせ解より速くなることは理解できます。また、S/Fの値が大きいところで、4段研磨の適切な組み合わせ解が3段研磨の適切な組み合わせ解よりも速くなり、また同様にS/Fの値が大きいところで、5段研磨の適切な組み合わせ解が4段研磨の適切な組み合わせ解よりも速くなることは推察されています。このことは厚いSから加工を始めて、より薄いFを目標とする場合はより多段の加工が優位になることを示しています。また、連載(3)の3-3.章で述べたように洗浄時間を考慮すると、より多段研磨が優位になる条件は、さらにS/Fの値が大きい方にシフトします。
5-5. 加工変質層の厚みの現象論的な関数が各段の加工時間に与える影響
連載(1)から連載(5)まで、個別の加工研磨工程を統合化して全工程時間を考察してきました。この考察の過程で、”加工速度と加工変質層の厚みの現象論的な関係”が、重要な因子だと想定して考察しました。加工速度と加工変質層の厚みの現象論的な関係を図5-1に示す3種類の関係に分類してみます。現象論的な関係式を表現すると、形式的には下記の(5-8)式のような式で近似しました。
Xn(vn) = βn vnq(n) (5-8)
Xn(vn)はn番目の加工工程で導入される加工変質層の厚みを示しています。vnはn番目の加工の加工速度です。q(n)は実数で、図5-1(a)はq(n)>1.0の場合です。(b)はq(n)=1.0, (c)はq(n)<1.0の場合です。βn は比例定数です。βnのディメンションは(5-8)式の両辺のディメンションを一致させるように設定します。q(n)が整数ではない場合は、βnのディメンションはちょっと厄介ですが、(5-8)式は単なる現象論的な式と割り切って考えます。
図5-2(a)のグラフは、加工速度を速くすると加工変質層の厚みが比例関係より上側方向にぶれる場合です。SiC研磨の研究開発の報告 [長屋ら、デンソーテクニカルレビュー 20 222 (2015)、ネットワーク上で閲覧可能書類] では、加工速度が速い領域で加工変質層の厚みが上側方向にぶれる加工研磨では、ウエハ表面にスクラッチやクラックが導入される場合が観察されるということが報告されています。加工変質層の厚みが厚くなってくる研磨条件、つまり図5-2(a)のグラフの上振れ領域では、普通は加工を行わないと思います。加工速度が比較的遅く上振れしない領域で加工を行う場合はq=1.0のように近似する加工になると考えられます。
加工速度を上げていっても加工変質層の厚みがあまり増えていかないないような加工、つまり図5-2(c)のような加工は、優秀な加工ではあると考えられますが、全体の加工速度を考えた場合、加工研磨工程が進むにつれ、加工研磨時間が長くなってきます。図5-2(b)の場合よりも速いのかは、話は簡単ではなく、それぞれの最適解は、d1,d2,d3,・・・や、a1,a2,a3,・・・などの定数の値に依存しています。これらのパラメタの実際の値を指定していない限り、どちらの場合が速いかは比較することができません。
実際の加工作業をシミュレーションする場合は、加工速度と加工変質層の関係を前もって調べておけば、PCを使って入力パラメタを振って色々と全加工研磨時間を計算し、力づくで比較することは可能だと思われます。
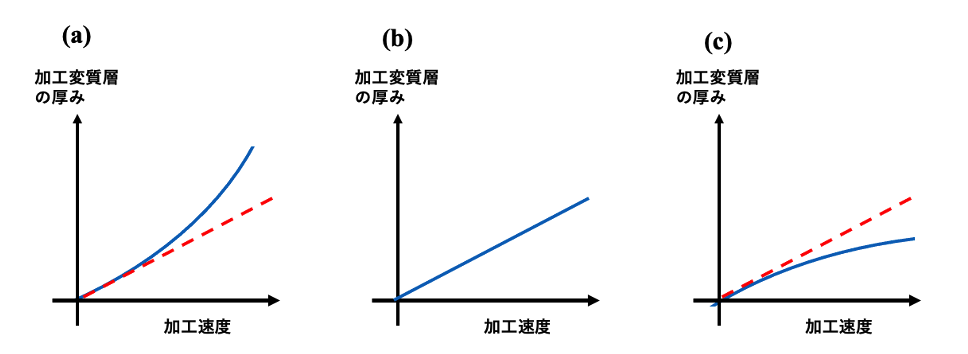
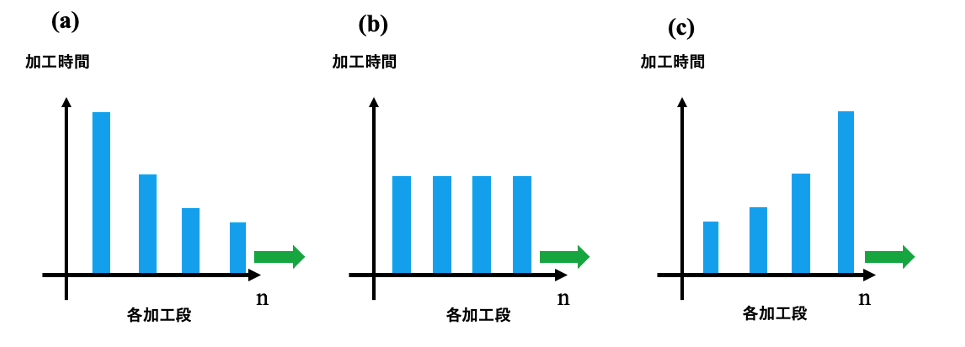
図5-2は、横軸は、各加工研磨段nを示し、縦軸は各加工段の加工時間を示します。図5-2(a),(b),(c)の各図の縦軸は同じスケールではありません。図5-2(a)は多段加工の全ての工程でq(n)>1.0の場合の各加工段の加工時間の長さを示しています。図5-2(b)は全ての工程でq(n)=1.0の場合の各加工段の加工時間の長さを示しています。図5-2(c)は全ての工程でq(n)<1.0の場合の各加工段の加工時間の長さを示しています。図5-2のような各研磨段の研磨時間の配分になることは、連載(2)のAppendixに示されている表の研磨時間から推察することができます。
実際の加工作業で、適切な条件で加工を行なっているのかは不明ですが、実際の各段の時間の割り振りは、図5-2(b), (c)のような割り振りが一般的だと思われます、これは加工速度と加工変質層の厚みの現象論的な関係が、図5-1(b),(c)のような関係の研磨を行なっていることを示唆している可能性があります。
5-6. まとめ
5段加工研磨モデルを考察しました。5段の工程を考慮すると実際の加工研磨工程に近づいてきました。加工研磨工程の段数をさらに増やし、6段工程や7段工程の解析解も可能だと思われますが、加工段数を増やしても同じような話が繰り返して出てくるので、加工研磨工程を増やす話はこれで終了します。加工段数を増やした場合は、帰納法的に推察はつくと思います。また段数をさらに増やす場合はPCを使って考察する方が現実的です。次回の連載で、加工速度、加工変質層の厚みの計測値ばらつきについて考察します。






