次に転位の周りの格子歪がどのようになっているかを考えてみます。図1-4 (a)は、4H-SiC基底面らせん転位の向きξとバーガース・ベクトルbの向きを模式的に示しています。らせん転位の場合、転位の向きξとバーガース・ベクトルbの向きは平行か反平行かの関係にあり、転位の周囲の歪は剪断歪のみが存在していて、圧縮歪みや膨張歪みは伴っていないことになっています。格子歪の向きはバーガース・ベクトルbの向きに沿って発生しています。このバーガース・ベクトルの方向と垂直な方向を向くgベクトルの反射を選んで暗視野像や暗視野像を観察すると転位は見ることができません。
図1-4 (b)は 4H-SiC基底面刃状転位の向きξとバーガース・ベクトルの向きbを示しています。この図のような刃状転位の周囲の歪みを見ると、転位近傍の転位の上側方向では4H-SiC結晶の単位胞の大きさは圧縮されており、転位の下側では単位胞の大きさは膨張されていています。それらの歪の方向はバーガース・ベクトルの向きbの方向です。また、刃状転位の場合、転位の向きとバーガース・ベクトルの向きとの両方に垂直な方向、つまり図のc軸方向にも小さな格子歪δを伴っています。刃状転位の場合はbに垂直なgベクトルを選んで観察しても、δベクトルの変位による、転位のコントラストが現れます。gベクトルが、bに垂直で、なおかつδベクトルに垂直であれば、刃状転位が存在していてもコントラストは現れません。
実際の基底面転位は基底面らせん転位でも基底面刃状転位でもない基底面混合転位の場合が多いのですが、そのような基底面混合転位は、基底面らせん転位と基底面刃状転位の歪成分を足し合わせたような歪を伴っています。以上の結果をまとめると、転位のコントラストは、バーガース・ベクトルや、転位の向き、gベクトルに依存して、現れたり、消えたりすることがわかります。
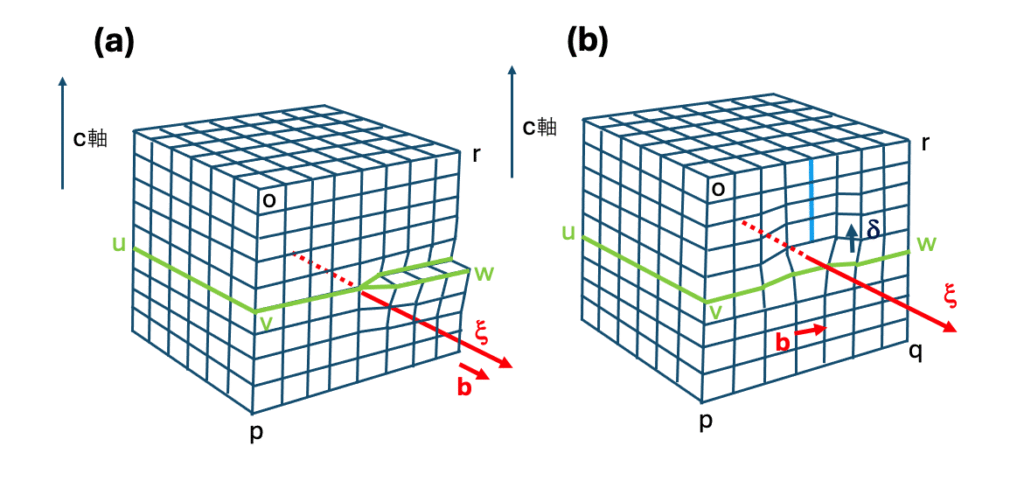
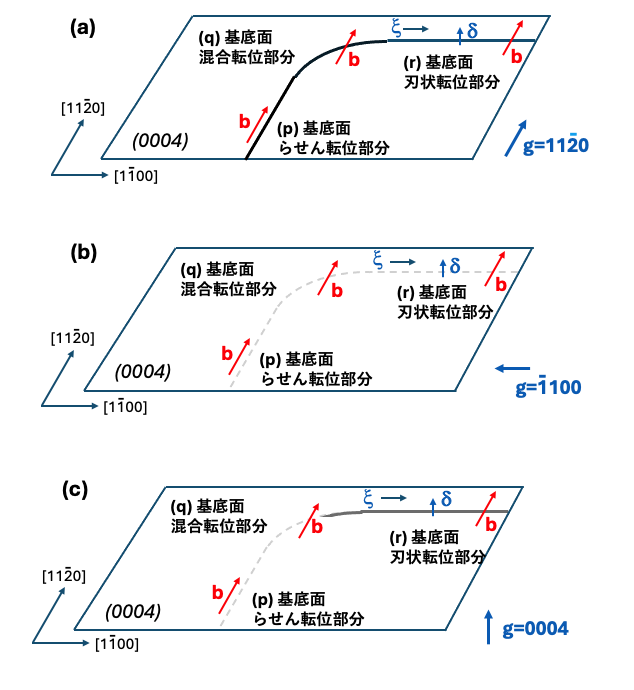
図1-5は転位のコントラスが現れるのか、存在していても見えていない状態なのかを示す説明図です。図はb=a/3[1120]の基底面転位が蛇行し、転位の向きが変化している状態を模式的に示しています。それぞれ、(p) 基底面らせん転位部分、(q) 基底面混合転位部分、(r) 基底面刃状転位部分を示しています。図1-5 (a)は g・bが値をもつ場合を示しています。転位のコントラストが出現するので、転位が存在していることは確認できます。図1-5 (b)は g・b=0, なおかつg・δ=0の場合を示しています。転位は存在していても、コントラストは出現せず、転位の存在を認識できない状態です。図1-5 (c)は g・b=0, そしてg・δ≠0の場合を示しています。刃状転位の場合、コントラストは現れます。この場合、転位の向きと、バーガース・ベクトルに垂直な向きの歪み成分がコントラストを出現させています。基底面らせん転位のコントラストは消えています。また、刃状転位に近い混合転位もコントラストを示します。基底面らせん転位の存在は認識できません。
図1-5(c)の0004反射を利用して観察する場合、観察する方向は断面観察の場合で、幾何学的に考えて図のように0004面を俯瞰的には観察できないのですが、図1-5(c)はg・δが値をもつ場合の観察の説明のため0004面の俯瞰的なイメージを示しています。