Appendix 1（2, 3）
結晶の対称性を議論する際に必要となる基本情報を以下にまとめておきます。
- 格子とは
結晶中で同じ周囲環境となる位置を点で表したもの。その点を格子点と呼び、格子点の集合が格子である。格子点の取り方には任意性があり、格子点に必ず原子がある必要は無い。また格子全体は、格子点を頂点とする適切な平行六面体の集合として表現できる。この平行六面体をユニットセルと呼ぶ。平行六面体の選び方にも任意性があるが、ユニットセルの内、体積最小でその中に格子点を１個（辺や頂点にある格子点は共有するユニットセルで分割）含むものを基本ユニットセルという。平行六面体を表現するには、１頂点を共有する三辺をその頂点を始点とするベクトルとして扱い、a軸、b軸、c軸（右手系が標準）とする。a軸、b軸、c軸に対応するベクトル（並進ベクトル）の長さをa, b, c、その間の角度をα, β, γとしてこれらを格子定数と呼ぶ。通常ユニットセルは、極力その対称性が高まるように選ぶ。基本ユニットセルの三辺を表すベクトルを基本並進ベクトルと呼ぶ。
- 基本要素（モチーフ）とは
結晶中で、格子点に配置される原子等（原子やイオン、或いは分子）の集団。対称性を議論する際には、基本要素の範囲を適切に定義することが重要。その集団内のある１点のまわりの対称性で特徴付けられる。
- 結晶構造とは
結晶内の原子等の配置を表したもので有り、格子及び、すべての格子点に等しく配置される基本要素（原子等の集団）を定義することで表現できる。即ち
結晶構造 ＝ 格子 ＋ 基本要素（モチーフ）
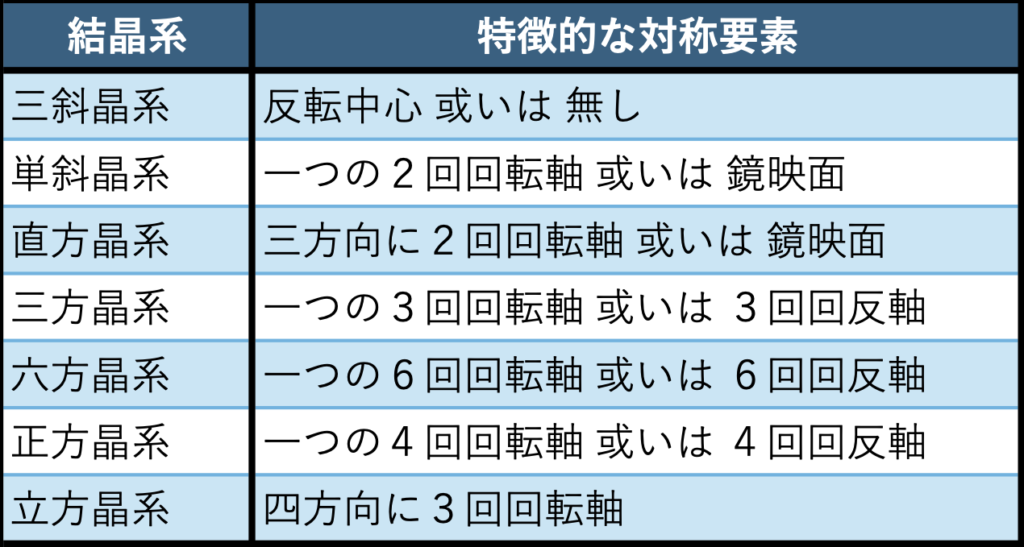
結晶中では、基本並進ベクトルに関する並進対称性と格子点周りの対称性が維持され、結晶構造はこの対称性で特徴付けられる。
- 格子構造
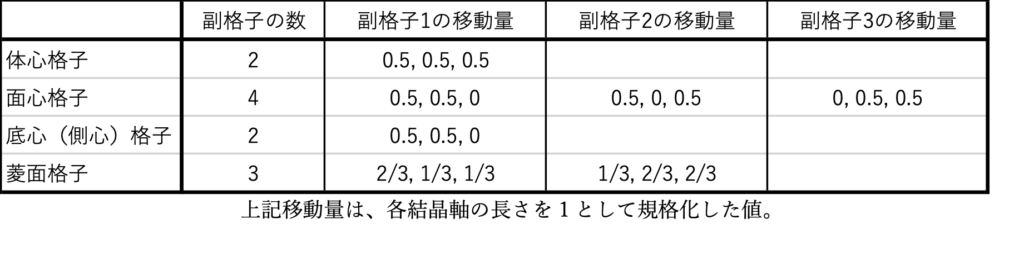
格子の構造はそれを構成する格子点の配置で決まるが、平行六面体である単純格子とそれを並進対称性が保たれるように平行移動（センタリングと称する）させた上で合体させ（もとの単純格子並びに平行移動させた単純格子を副格子という）、格子全体を人間が慣習的に想像しやすいようにした複合格子に分類される。複合格子には、体心格子、面心格子、底心（側心）格子、菱面体格子の４種がある。ユニットセルが複合格子の場合、対称性は落ちるがより体積の小さい基本ユニットセルに分解できる。複合格子では、通常基本ユニットセルよりも複合格子をユニットセルとして扱い、それを定義する三つのベクトルから格子定数を定義する。各複合格子における副格子の数と移動量を下記に示す。
- 格子の対称性と結晶系、Bravais格子
格子はその対称性（a, b, c, α, β, γ の関係）から、三斜晶系、単斜晶系、直方（斜方）晶系、正方晶系、六方晶系、三方晶系、立方（等軸）晶系の７種に分類され、それぞれ特徴的な結晶点群対称操作を持つ。格子の種類と晶系の組み合わせから等価なものを除いて、Bravais格子と呼ばれる１４種の格子が導かれる（下図参照）。六方晶単純格子の図に示される六角柱は、複合格子でも(基本)ユニットセルでもないこと、菱面体格子は単純六方格子の複合格子としても表現できるが、通常は赤線で表されたその基本ユニットセル（青線で表された四角柱は人間に理解し易くした基本でないユニットセルである）が属する三方晶系として扱われることに注意。また、単純三方格子においては、γがある特殊な値を取るとき、より対称性の高い別のBravais格子となる。具体的には、cos γ = 0（γ = 90˚）の時が単純立方格子、1/2（γ = 60˚）の時が面心立方格子、-1/3（γ = 109.47˚）の時が体心立方格子である。単斜晶系においては、慣例上γ ≠ 90˚とする場合と、β ≠ 90˚とする場合がある。下図ではβ ≠ 90˚として記載している。各結晶系に特有の対象要素を同時に示す。
