アイシーソルーションズ, LLP

4-1. はじめに

前回の連載の(3)では、3段プロセスの最適条件について解析的な解を求めました。2段研磨より3段研磨の方が速くなる条件などを考察しました。今回は4段の加工研磨プロセスについて同様の考察を行います。

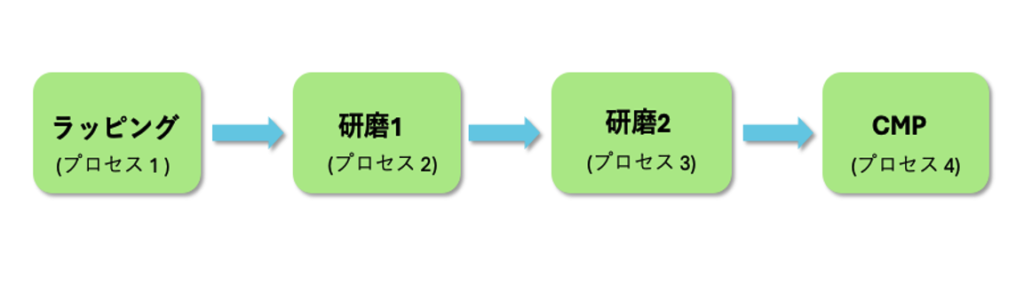
図4-1はウエハ表面の加工プロセスの例を示しています。4段工程まで増やすと実際の加工研磨工程に近い状態になってきます。図4-1に示している各プロセスの後、ウエハの洗浄を行い各プロセスの際に発生した研削屑や砥粒屑などを取り除きます。3段プロセスの後CMPを行い加工変質層を薄くする4段工程を考察します。粗いラッピングも、2段ダイアモンド研磨も、CMPも、同じ研磨のモデルを使います。つまり、加工速度と加工変質層の関係は、(A)式、X_n (v_n) =  a_nv_n 、あるいは(B)式、X_n (v_n) = d_n v_n ^1/2 、を使って考察します。

4-2. 4段研磨の最適解

3段研磨の場合と同様に、4段研磨の全研磨時間は、洗浄時間を除いて

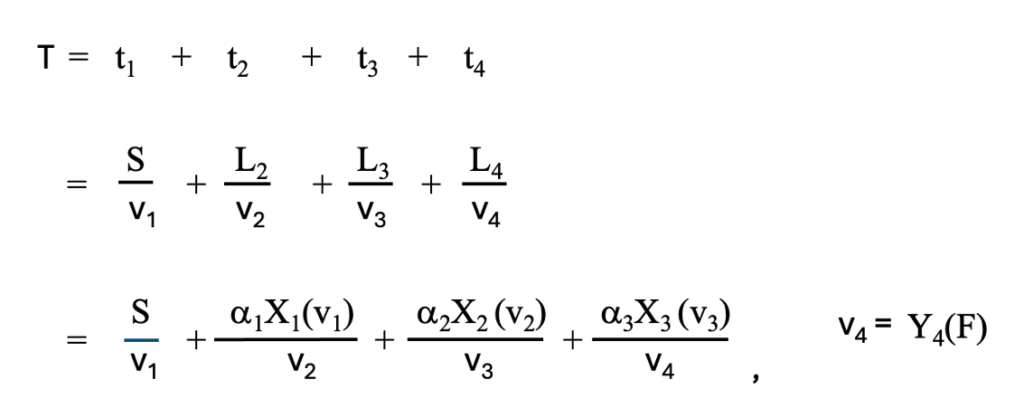
(4-1)

で示されます。ここで、t₁,t₂,t₃,t₄は4段のそれぞれの研磨時間、v₁,v₂,v₃,v₄は4段のそれぞれの研磨速度、Sは1段目の研磨での削り落とす目標の厚みです。Fは最終の目標として到達する加工変質層の厚みです。

X_n(v_n), Y_n(F)は実験によって前もって調べられている加工変質層の厚みと研磨速度の関係を、現象論的に示す関数です。α_nは安全係数です。v₄の値は、最終仕上げの状態FでY₄(F)と一意的に決定されています。

 (4-1)式に各関数や各値を代入し、エクセルなどのPCソフトを使って、v₁,v₂,v₃,の3つのパラメタを変化させTを計算すると、Tの最小値を求めることができます。その時のv₁,v₂,v₃,や、t₁,t₂,t₃,t₄も決定することは、このモデルで可能です。ここでは解析的解を使って色々と考察します。

4-3. (A)式を用いた4段研磨の最適解

3段研磨の場合と同様に、4段研磨の最適解を解析的に求めます。加工変質層の厚みと研磨速度の関係は、(A)式を想定します。

P_n = X_n (v_n) =  a_nv_n 　　                　(A)

この場合の、(4-1)式の4つの項のうち、後ろの3つの項の最適解は、すでに3段研磨の考察で示されていて、(3-5)式で表現されます。3段研磨の最適解を使った4段研磨の研磨時間は以下のように示されます。(4-2)式の第1項は1段目のプロセスの時間、第2項は、2段目工程から4段目工程の最適解です。(4-2)式のT_Lは4段研磨の研磨時間のlocal minimumを示しています。T_Lはv₁の関数になっています。

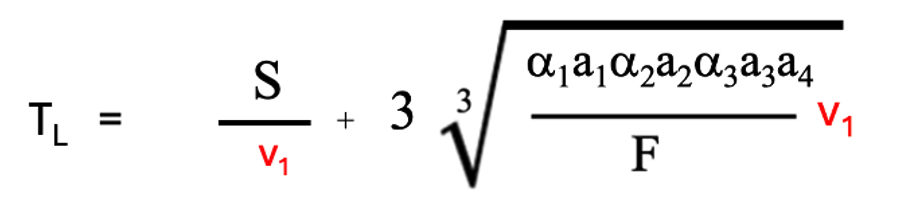
(4-2)

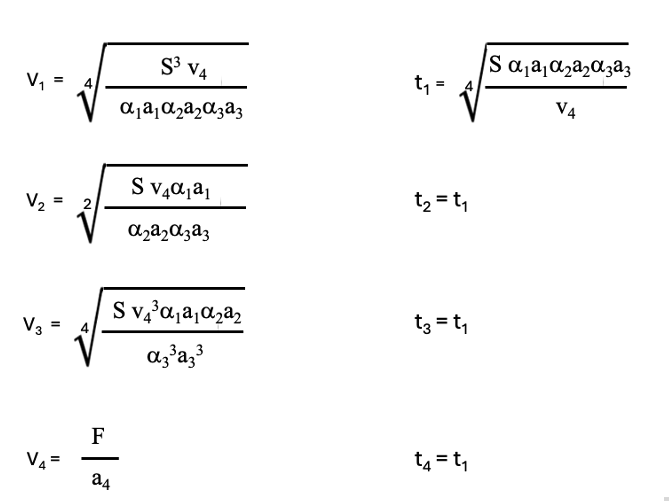
(4-2)式は、今まで見てきた(1-5),(3-3)式と同じようにv₁の増加に伴い第1項は減少し、第2項は増加します。(4-2)式をv₁で微分しT_Lの最小値を求めると、以下の最適解を求めることができます。

(4-3)

加工変質層の厚みと研磨速度の関係に(A)式を想定した場合、2段研磨、3段研磨と同様にt₁ = t₂ = t₃ = t₄の関係が求められます。この結果は前回の連載の(3-4)式からも帰納的に推察される結果です。3段研磨の場合と同様にv₄はFを設定すると固定されています。洗浄時間WTを考慮すると4段研磨の全研磨時間は

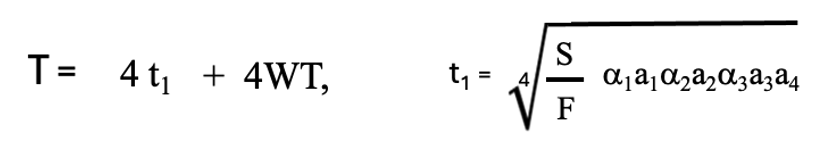
(4-4)

というふうに全研磨時間の最適解が一意的に決まります。また、各研磨段に対して最適な研磨速度、研磨時間の解が存在しているという事がわかります。3段研磨で考察されたように、これらの4段研磨の解が意味を保つためにはS>>Fなる条件が必要かと推察されます。

ページ : 1 2 3