4-4. (B)式を用いた4段研磨の最適解
次に、加工変質層の厚みと研磨速度の関係は、(B)式を想定して考察します。(B)式は以下のような式です。
Pn = Xn (vn) = dn vn 1/2 (B)
(4-2)式と同様に4段研磨のlocal minimum TLは洗浄時間を考慮せずに以下のようにv1の関数として示されます。
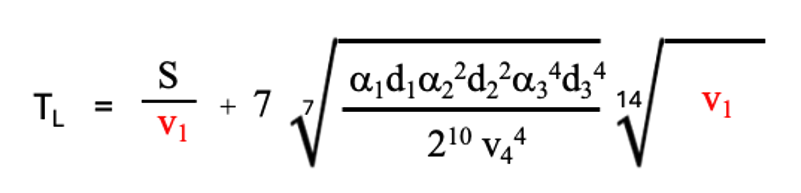
(4-5)
(4-5)式から、この場合の4段研磨最適解が以下のように求められます。
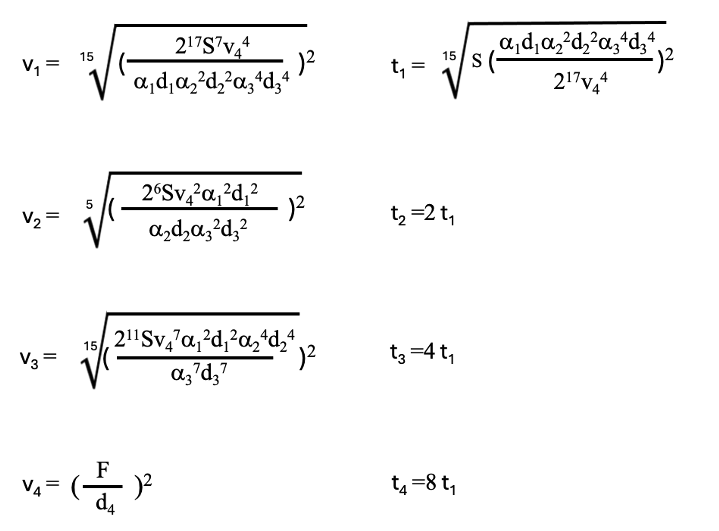
(4-6)
3段研磨の場合から推察されるように、各段の加工研磨時間はt2=2t1, t3=4t1 t4=8t1と求められます。また、v4はFを設定すると最初から固定されています。4段プロセスの最適解は4回の洗浄時間WTを含めて下記のように一意的に決定されます。
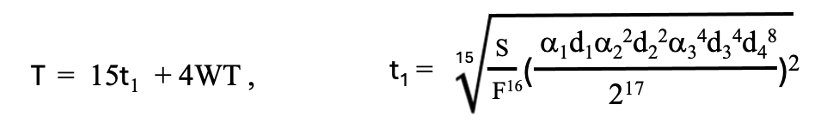
(4-7)
3段研磨で考察されたように、これらの4段研磨の解が意味を保つためにはS>>Fなる条件が必要かと推察されます。
4-5. (A)と(B)式の混在する状態での考察
加工速度と加工変質層の現象論的な関係式として(A)式を用いる場合や、(B)式を用いる場合を考察しました。そして、全研磨工程の最適解としては一意的に解が存在することが示されました。図4-1に示す4段プロセスの図では、初段はラッピングプロセス、終段はCMPです。(A)式を用いた解析的な解では、すべての4つのプロセスで (A)式が成立していることを想定しています。また、(B)式を用いた解析的な解では、すべての4つのプロセスで (B)式が成立していることを想定しています。おおらかに考えて、そのような想定で、考察が可能だと思われますが、各プロセスでは利用する装置が異なったり、研磨剤、砥粒が異なり、使用方法が異なっている場合があります。そういう場合、研磨速度と加工変質層の関係は、各段で色々と異なってくると推察されます。そこで、1段目のラッピングでは (A)式を用いて、残りの3段プロセスでは (B)式を使う場合を想定してみます。また最初の3段プロセスでは、(A)式を用いて最後の4段目CMPプロセスのみ (B)式を使う場合などを想定して解析的に考察すると、どのようなことがわかるかを考察してみます。これらの考察では、粗い研磨の場合は (A)式を、精密な研磨の場合は(B)式を使うことを想定しています。
4-5-1. 初段に(A)式を想定し、残りのプロセスでは(B)式を想定する場合
最初の2つの加工段は、(A)式を用いて求めた2段研磨の最適解(1-6)式を使って表現します。
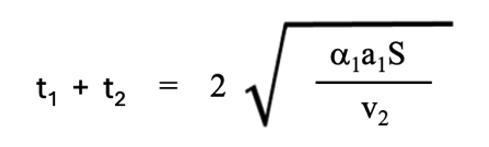
次に、残りの3段と4段は(2-4)式を使って表現することができます。
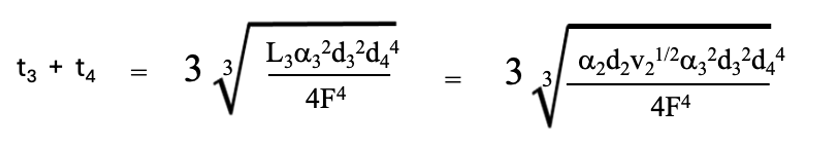
L3 は3段目の研磨で削り落とす深さです。4段研磨の時間は以下の式で示すことができます。
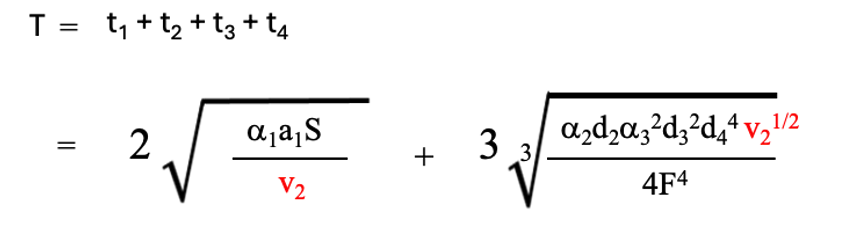
(4-8)
この式はv2の関数になっています。
(4-8)式で示されるTとv2の関係をグラフで描くと、図2-2と似たような図を描くことができて、Tの最小値が存在することがわかります。Tをv2で微分してTの最適解を求めます。以下のような最適条件が得られます。

(4-9)
上記の最適条件で各プロセス段での時間を見ると、t2=t1, t3=2t1, t4=4t1 のような関係を求めることができます。この考察では、(1-6)式の解、(2-4)式の解を利用して求めているので、こうなることはある程度予測されます。しかしながら(4-9)式のt1は(4-3),(4-6)式のものとは異なる値になります。最終的に4段研磨の全研磨時間は各加工研磨の終了時に行われる4回の洗浄時間WTを考慮すると、以下のようになります。
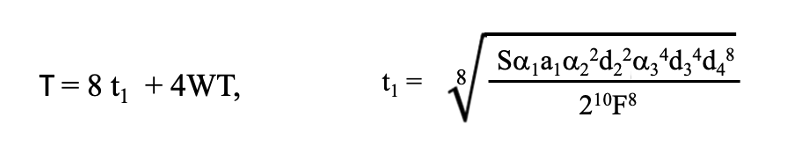
一意的な解が求められます。これらのことより、加工速度と加工変質層の厚みの関係を前もって調べていると、4段プロセスの全加工時間は推察がつくことがわかります。






