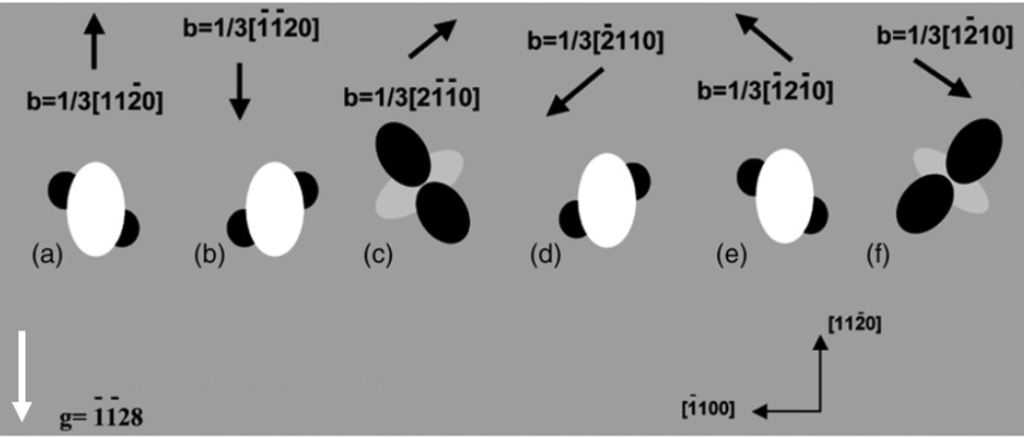
紛らわしいことに図6-3の(a)と(e)はコントラストが良く似ています。また、図6-3の(b)と(d)も良く似ています。g=1128の回折条件のみでは、これらを区別することは困難なように思います。
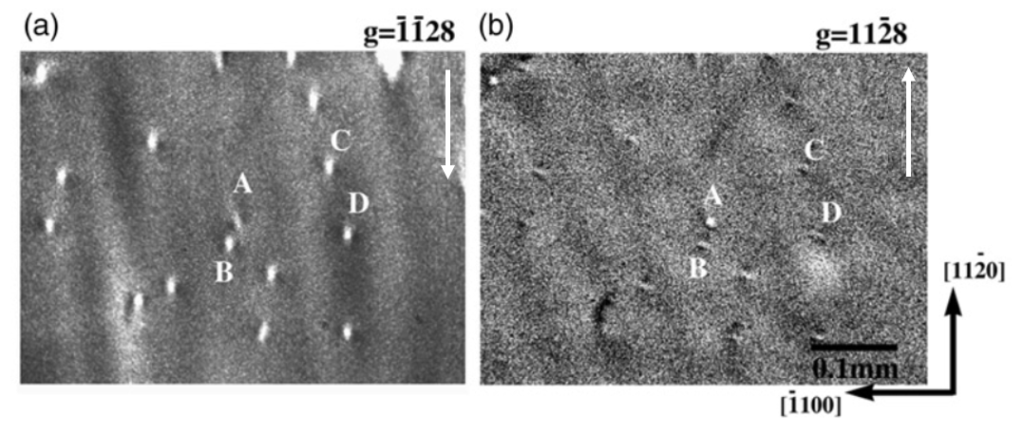
図6-4はgベクトルを変えると貫通刃状転位のコントラストがどのように変化するかを示した像の一例です。(a)はg=1128の観察例です。貫通刃状転位”A”のコントラストを見ると図6-3(b)のコントラストと似ていますが、図6-3(d)のコントラストとも似ていて紛らわしいです。また、図6-4(a)の貫通刃状転位”B”、”C”、”D“は、図6-3(a) のコントラストと似ていますが、図6-3(e)のコントラストとも似ていて紛らわしいです。図6-4(b)はg=1128の場合の像です。ウエハ表面に投影したgベクトルの向きは逆向きになります。b=1/3[1120]の貫通刃状転位のコントラストはg=1128では図6-3(b)のコントラストを示しますが、g=1128では、図6-3(a)と良く似たコントラストを示すことが単純に推察されます。図6-4(b)を見ると貫通刃状転位”A”は、図6-3(a)と似たコントラストを示しています。このことより貫通刃状転位”A”はb=1/3[1120]であることがわかります。一方、貫通刃状転位”B”、”C”、”D“が、もしもb=1/3[1120]ならば、g=1128の場合、貫通刃状転位”B”、”C”、”D“は図6-3(b)と似たようなコントラストを示すはずですが、そのようなコントラストは示していません。貫通刃状転位”B”、”C”、”D“はb=1/3[1210]であることがわかります。2つの異なる反射の像を見比べることによりバーガース・ベクトルを一意的に同定することは可能です。貫通刃状転位のバーガース・ベクトルを同定するには、最低2つの反射、g=1128、g=1128は必要と思われます。
放射光ベルク・バレットX線トポグラフ像に現れるSi面側の貫通刃状転位の像コントラストは定性的的に一応図6-3に示すように分類しています。実際に観察される像は、いろいろな方向に少し圧縮されていたり、引き伸ばされていたりします。透過型電子顕微鏡で貫通刃状転位を観察すると転位の向きが綺麗にc軸方向に向いておらず、いろいろな方向に少し蛇行していることが観察されます。これらの転位の向きに微小なばらつきがあることが、実際に観察されるトポグラフ像では、いろいろな方向に少し圧縮されていたり、引き伸ばされているように観察されるのではと推察します。また、これらのコントラストは、表面近傍で転位の周囲の歪が解放され、新たな格子変位がさらに加わっている効果も加わっているものと考えられます。、X線の出射面と回折を起こしているX線の波数ベクトルとのなす角度が、選ぶべき反射によって変化するので、それらの効果によっても、観察される像コントラストの一方向への伸びや縮小が発生すると考えられます。
蛇足的な話ですが、図6-1(a), (b)などでは基底面転位のコントラストの幅が大変広い状態が観察されています。これは基底面転位が拡張していることを示しているわけではありません。その(4)図4-1, 4-2(a)で示されている画像記録装置とSiCウエハの距離を離すと、黒い転位、白い転位、両方の基底面刃状転位の幅が広くなっていきます。入射X線が小さな発散角を持っていて、基底面転位のまわりの結晶格子の湾曲しているため、回折を起こして結晶の外に出てきたX線も小さな発散角を持っていると考えられます。この効果によって、画像記録装置を試料から離して行くと基底面刃状転位の幅が広くなると考えられます。通常、我々は30 cm程度の位置に画像記録装置を配置していました。画像記録装置を試料に近づけて行くと、転位のコントラストの幅が細くなっていきます。







コメントを残す