多数枚のショックレー型積層欠陥のコントラスト
SiCはN濃度にも依存しますがショックレー型積層欠陥のエネルギーが低いので、何らかの原因でショックレー型積層欠陥が局所的に多量に導入されていることがあります。ショックレー型積層欠陥が2枚導入された状態を想定してみましょう。この状態を図8-2に示します。2枚のショックレー型積層欠陥は近い所に位置していると想定し、部分転位Aとは逆のバーガース・ベクトルを転位Bは持っているとします。積層欠陥Aの上側の結晶を第1結晶、積層欠陥Aの下側が第2結晶、積層欠陥Bの下側の結晶を第3結晶とすると、第2結晶は第1結晶から見るとR=-bの変位を持っているので、積層欠陥Aのコントラストが積層欠陥観察可能部分と図中で示された部分では観察することができます。第3結晶は第1結晶から見るとR=0となって、二つの積層欠陥の距離が近いと表面から見た2つの積層欠陥が重なりあった部分で積層欠陥のコントラストが消失します。重なり具合の頃合いがちょうど良い場合、積層欠陥Aは両端に部分転位Aと部分転位Bを持ち、部分転位Bによって終端されていて、部分転位Bの右側の積層欠陥コントラスト消失部分には積層欠陥コントラストは観察されず、積層欠陥は1枚のみ存在しているように観察されるかもしれません。こういうことはトポグラフ像を見ると、部分転位Aと部分転位Bのバーガース・ベクトルを見ると何か変だと気付かされます。部分転位AとBの距離が近いとこれらの転位の長範囲の歪みは相殺され、観察されにくい状態、あるいは転位のコントラストの消失も考え方られます。
次に、ショックレー型積層欠陥3枚が近接して存在する場合を想定した場合を図8-3に示します。今度は3つの部分転位とも同じバーガース・ベクトルを持つと仮定します。一枚目の積層欠陥Aの場合、2πg・R =-2π/3だと想定します。この場合も部分転位Aと部分転位Cの間の積層欠陥のコントラストは現れます。部分転位Cより右側では、一番上の結晶と積層欠陥Cの下側の結晶では、トータルの変位で2πg・R =-2πとなって、回折を起こしている結晶面の1周期分の変位が発生し、積層欠陥は無かったことにして下さいと言われてしまい、積層欠陥のコントラスト消失が発生します。3本の部分転位は観察されていますし、部分転位のバーガース・ベクトルを調べると、これは変だと気が付きます。
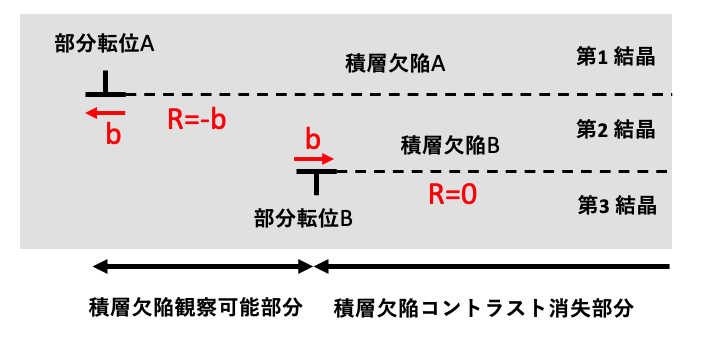
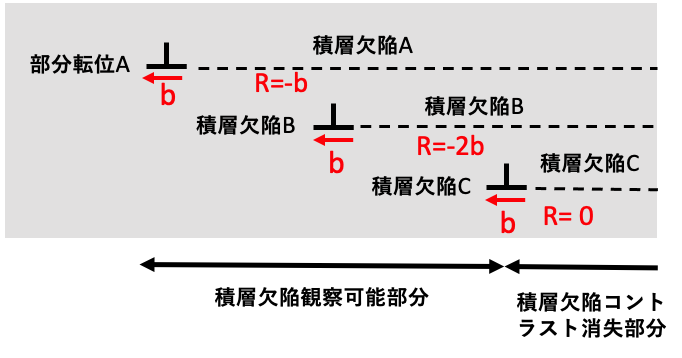
図8-3の例は、透過型電子顕微鏡法の教科書などで、積層欠陥の解析の話ではよく出て来る積層欠陥のコントラスト消失の典型的な話です。この典型的な話とは別に4H-SiCの3枚の近接したショックレー型積層欠陥では別の面白い事がそれなりに発生していると考えられます。3つのショックレー型積層欠陥の変位ベクトルがそれぞれ3つの異なる方向を向いていると想定します。例えば、R1=1/3[0110], R2=1/3[1100], R3=1/3[1010] とすると、3つの変位ベクトルは異なる3方向を向いていて、その総和は相殺され、図8-3の一番上の結晶と一番下の結晶の間の関係はR=0となってしまい、ウエハ表面から見た際に3枚の積層欠陥が重なっている部分の積層欠陥のコントラストは消失します。
図8-2や図8-3の例を考えると、ショックレー型積層欠陥が偶数枚重なっている時も、奇数枚重なっている時も、それぞれの積層欠陥の変位ベクトルRのつき方に依存して、重なっている部分の積層欠陥のコントラストが消失する可能性が考えられます。
同様なことを考えるとさらに多層枚のショックレー型積層欠陥のトポグラフ像のコントラストについて考察が可能です。しかしながら4H-SiCのエピ層中では、もう少し複雑で困ったことが発生していることが度々観察されます。以下に説明します。
複数枚ショックレー型積層欠陥集合体のコントラストおよびステルス積層欠陥
以前にも紹介しましたが、我々は4H-SiCのプロジェクトで、エピ層中やデバイス中の格子欠陥を調べるのに、顕微PL法→放射光トポグラフ法→FIB→透過型電子顕微鏡観察を行っていたことがあります。顕微PL法ではエピ層中に三角形状の積層欠陥をそれなりの密度で検出していました。しかしながら、それら積層欠陥のうち放射光X線トポグラフ法では全く検出できない物が一定比率存在していました。gベクトルを色々と変えて観察してもX線トポグラフ像ではこれらの積層欠陥はコントラストを現すことはありません。X線トポグラフ像では見ることができないと言うことは、同じ原理を使っている透過型電子顕微鏡のg・b解析でも観察することはできず、つまり見ることができないと言うことです。ただし断面試料を作製して透過型電子顕微鏡で高分解能像観察を行えば観察することは可能です。
これらのステルスな積層欠陥は、積層欠陥の縁に存在する部分転位も、コントラストの検出はできません。積層欠陥集合体を構成するそれぞれの積層欠陥の縁に存在する複数本のショックレー型部分転位は近接している場合が多く、近接する複数の部分転位のバーガース・ベクトルの和が相殺されているためです。積層欠陥の縁に存在する複数のショックレー型部分転位のバーガース・ベクトルの総和が0になることと、複数枚のショックレー型積層欠陥の集合体の変位ベクトルがR=0になることは矛盾の無い話です。近接して存在するショックレー型部分転位のバーガース・ベクトルの総和が相殺されていると、転位の周りの長範囲の歪みが相殺され、放射光X線トポグラフ法や透過型電子顕微鏡法のg・b解析では検出できません。断面試料の透過型電子顕微鏡や走査透過型電子顕微鏡を使った高分解能像観察、HAADF-STEM, ABF-STEM法では転位のコア構造を見ることができるので、隣接する複数のショックレー型部分転位の集合や、複数のショックレー型積層欠陥の集合体を観察することは可能です。
多数枚ショックレー型積層欠陥の検出の場合、とりあえず存在しているかどうかを簡単に調べるには顕微PL法が最適で簡単だと思います。ちなみに透過型電子顕微鏡や走査透過型電子顕微鏡を用いて、高分解能像観察、HAADF-STEM, ABF-STEM法でこれらの構造を調べる場合、積層欠陥の縁に存在している部分転位部を観察すると解析が容易になると思いますので、多数枚のショックレー型積層欠陥の構造を解析する際には部分転位部を観察することをおすすめします。
以上で、ベルク・バレットX線トポグラフ像で観察されるショックレー型積層欠陥の像と観察されないショックレー型積層欠陥のコントラストの掟の話をしました。次回以降はフランク型積層欠陥の像について説明します。







コメントを残す